R para Entomologistas: nível básico


CAPÍTULO 4

Aplicações de MLG para dados entomológicos de contagem

 

José Bruno Malaquias, Jéssica Karina da Silva Pachú, Filipe Lemos Jacques, Paulo Eduardo Degrande

 

https://doi.org/10.4322/mp.2020-12.c4

 

Resumo

Apresentamos nesta última seção, dois exemplos de dados que são de natureza discreta. Para isto, lançamos mão do teste de ajuste de Modelos Lineares Generalizados (MLG) com as seguintes distribuições: Poisson; quase-Poisson e Binomial Negativo. Um dos bancos de dados apresenta apenas um fator, enquanto o segundo banco de dados é constituído de um fatorial. Utilizaremos os seguintes pacotes do R: readxl, hnp, MASS, multcomp e Rmisc. Os comandos a serem executados no R estão sendo apresentados com a cor azul.

Palavras-chave: deviance; variável discreta; número de insetos; contrastes; glm.


1. Importação do banco de dados - exemplo 1

O banco de dados a ser trabalhado, trata-se da ocorrência de Scaptocoris castanea Perty, 1830 (Hemiptera: Cydnidae) em diferentes culturas. Para acessar o banco de dados clique aqui, o banco de dados também está exposto no anexo desse capítulo.

Host é a planta hospedeira;

Rep corresponde a bloco (repetição) e

y é a variável resposta que foi estudada como sendo a ocorrência dos insetos.

Antes de iniciarmos a análise devemos rodar o comando: rm(list=ls(all=TRUE)) que serve para limpar a memória do programa e evitar erros.

Depois de alterar o nosso diretório (selecionar a pasta que contém os arquivos que utilizaremos): Session -> Set working Directory -> Choose Directory

Podemos visualizar os nomes de todos os arquivos que contén na pasta selecionada: list.files()

Em seguida devemos usar o comando para carregar o pacote que lê a planilha do Excel, que é o pacote readxl [1]: require(readxl)

Depois de carregar o pacote, precisamos ler o arquivo, para isso usaremos a linha de comando:

data<-read_excel("Dados-Abundancia.xlsx", sheet = 1)

data é o nome dado ao dataframe (você pode colocar o nome que quiser);

read_excel é o comando para ler o arquivo do Excel;

Dados-Abundancia é o nome do seu arquivo dentro da pasta selecionada;

xlsx é a extensão do arquivo com o qual você está trabalhando;

sheet = 1 faz referência a qual aba do seu arquivo do Excel quer analisar.


2. Análise descritiva

O primeiro passo é a produção de uma análise descritiva, para isto utilizaremos o pacote Rmisc [2], para carregar o pacote usaremos o comando: require(Rmisc).

Em seguida com a função summarySE, iremos obter os valores médios, desvio padrão, erro padrão e intervalos de confiança associados à média, para isso devemos rodar a linha de comando:

(descritiva<- summarySE(data, measurevar="y", groupvars=c("Host")))

O resultado da análise descritiva segue abaixo:

O próximo passo é a escolha do modelo que melhor se ajusta a esse conjunto de dados.


3. Teste de ajuste dos modelos

Quando a variável é independente precisamos verificar se as mesmas são fatores, para isso utilizamos o comando:

is.factor(data$Host)

A resposta para a verificação precisa ser: TRUE

Caso a resposta de: FALSE, é necessário converter as variáveis independentes em fatores, para isso utilizamos a função "as.factor": data$Host<-as.factor(data$Host)

Em seguida é necessário verificar se a conversão foi bem sucedida: is.factor(data$Host)

Com a conversão bem sucedida, podemos analisar qual dos 4 modelos melhor se ajusta aos dados, para isso utilizaremos os modelos:

model1<-glm(y~Host+Rep, data=data): Modelo gaussiano (sem necessidade de testar esse modelo, pois ele é aplicado à variáveis contínuas.

model2<-glm(y~Host+Rep, family="poisson", data=data): Modelo Poisson.

model3<-glm(y~Host+Rep, family="quasipoisson", data=data): Modelo quase-Poisson.

Alguns modelos precisam de pacotes específicos (como o model4, modelo binomial negativo). Para isso é necessário carregar o pacote MASS [3] para trabalharmos com a função glm.nb

Require(MASS)

model4<-glm.nb(y~Host+Rep, data=data): Modelo Binomial Negativo.

Em seguida é necessário carregar o pacote "hnp" para analisarmos a qualidade de ajuste dos modelos aos dados, usamos: require(hnp), o pacote hnp foi desenvolvido por Moral et al., [4], para maiores detalhes sobre envelope simulado meio normal, consulte Demétrio [5] e Demétrio et al., [6].

Para visualizarmos os gráficos em outra janela usamos o comando: dev.new()

Para agrupar os 4 gráficos em um grid 2 x 2: par(mfrow=c(2,2))

Para testar o ajuste dos diferentes modelos utilizaremos diferentes linhas de comando:

hnp(model1, print.on="T", main="Normal"): Teste da qualidade de ajuste do modelo normal

hnp(model2, print.on="T", main="Poisson"): Teste da qualidade de ajuste do modelo Poisson

hnp(model3, print.on="T", main="QuasePoisson"): Teste da qualidade de ajuste do modelo quase-Poisson

hnp(model4, print.on="T", main="BN"): Teste da qualidade de ajuste do modelo Binomial Negativo

Esse é o resultado do ajuste dos modelos aos dados de contagem:

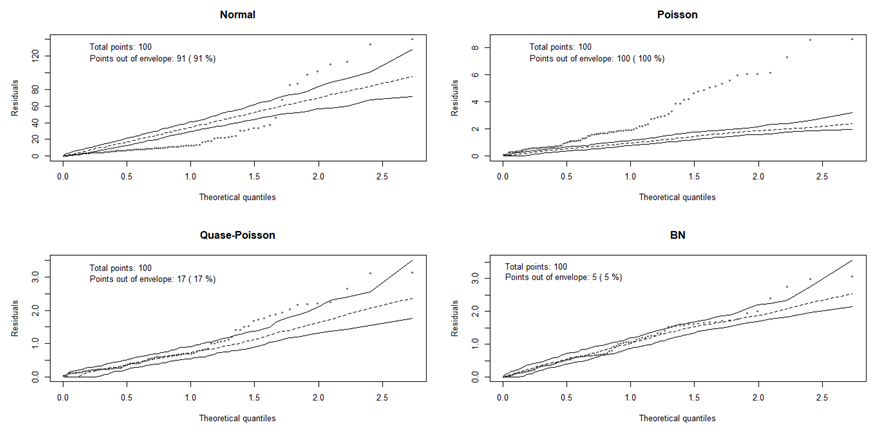
Percebe-se que o modelo Binomial Negativo (BN) foi o modelo que melhor se ajustou aos dados de contagem de S. castanea, pois ficaram apenas 5% dos pontos fora do envelope. Portanto, esse será o modelo selecionado.

O próximo passo é rodar o comando anova com teste F para mostrar a análise de deviance do modelo selecionado. Para isso, utilizaremos o comando:

anova(model4, test="F")

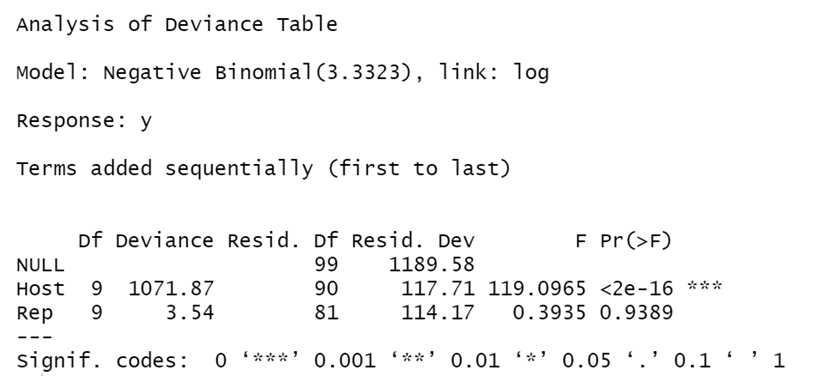
Conforme análise de deviance, é possível verificar que existem evidências de diferença significativa entre as plantas hospedeiras (fator host), pois Pr (> F) é inferior a 0,05 (5%).

Agora vamos comparar os tratamentos utilizando o pacote "multcomp" [7], para isso vamos rodar a linha de comando: require(multcomp)

Para visualizar as diferenças nós utilizaremos a função glht e o método Tukey, para isso é necessário rodar o comando:

(Comparações <- summary(glht(model4, linfct = mcp(Host = "Tukey"))))

Comparações <- summary(Comparações, test = univariate())

Em seguida vamos imprimir os resultados expresando as letras para cada tratamento:

(Letras.mP<-cld(Comparações, level=0.05, Letters= c(LETTERS, letters), decreasing=TRUE))

A partir do teste a cima obteremos como resultado as comparações, as que possuírem as memas letras são consideradas significativamente iguais:


4. Importação do banco de dados - exemplo 2

Exemplo 2 - Dados de contagem em um ensaio com estrutura de fatorial que tratou da contagem de Spodoptera frugiperda (Lepidoptera: Noctuidae) em diferentes plantas hospedeiras (fator 1) em dois estádios vegetativos (fator 2), para obter o banco de dados e script, clique aqui

Para ler os arquivos do Excel, precisamos do pacote "readxl" [1], para isso usamos o comando: library(readxl)

Para ler o banco de dados, usar o comando:

df <- read_excel("DadosContagem.xlsx", sheet = 1)

Para visualizar o cabeçalho: head(df, n=2)

Antes de seguir com as analises é necesario verificar se as variáveis sao fatores, para isso usamos o comando:

is.factor(df$Estadio): Perguntar se Estádio é fator

is.factor(df$Bloco): Perguntar se Bloco é fator

is.factor(df$Cultura): Perguntar se Estádio é fator

Caso a resposta seja "FALSE", é necessário converter as variáveis.

df$Estadio<-as.factor(df$Estadio): Conversão da variável Estadio a um fator

df$Bloco<-as.factor(df$Bloco): Conversão da variável Estadio a um fator

df$Cultura<-as.factor(df$Cultura): Conversão da variável Estadio a um fator

após a conversão é necessário verificar se deu certo.

is.factor(df$Estadio): Perguntar novamente se Estádio é fator

is.factor(df$Bloco): Perguntar novamente se Bloco é fator

is.factor(df$Cultura): Perguntar novamente se Estádio é fator

Se a resposta for "TRUE", podemos seguir com as análises

OBS: caso tenha dúvida sobre os passos descritos a cima, consultar os capítulos anteriores.


5. Teste de ajuste

Vamos testar o ajuste dos modelos Poisson, quase-Poisson e Binomial Negativo:

Modelo.poisson<-glm(SfrugTot~Estadio*Cultura+Bloco, family= "poisson", data=df)

Modelo.qpoisson<-glm(SfrugTot~Estadio*Cultura+Bloco, family= "quasipoisson", data=df)

library(MASS) - lembre-se que é necessário carregar esse pacote MASS [2] para testar o modelo binomial negativo.

Modelo.BN<-glm.nb(SfrugTot~Estadio*Cultura+Bloco, data=df)

Agora vamos testar se o modelo se ajustou aos dados, para isso vamos rodar o pacote hnp [3] com o seguinte comando:

require(hnp)

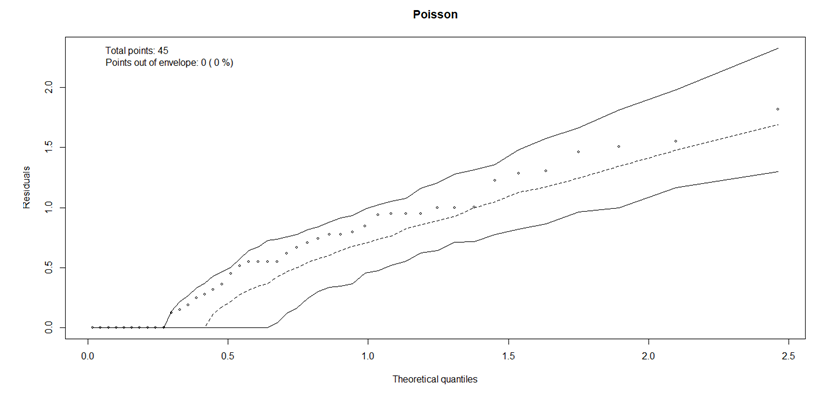
hnp(Modelo.poisson, print.on="T", main="Poisson")

É possível observar que o modelo Poisson se ajustou aos dados, pois nenhum dos pontos ficou fora das linhas, portanto, utilizaremos esse modelo.

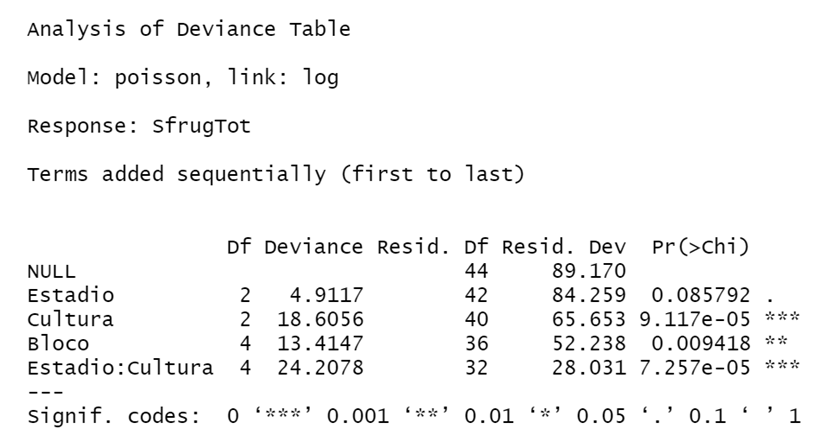
Após escolher o modelo, podemos rodar o comando ANOVA. Como o modelo de poisson se ajustou os dados, vamos usar o teste de qui-quadrado (Chisq):

anova(Modelo.poisson, test="Chisq")

Esse é o resumo da análise de deviance. É possível observar que houve interação sig- nificativa envolvendo os fatores Estádio e Cultura.

Analysis of Deviance Table - Model: poisson, link: log

Response: SfrugTot


6. Desdobramento da interação

Como a interação foi significativa, vamos realizar o desdobramento da interação, precisamos conhecer os níveis de cada fator. Para isto vamos utilizar a função sqldf do pacote sqldf [8]

sqldf::sqldf("select distinct Estadio from df"): Verificar os níveis do fator Estadio

sqldf::sqldf("select distinct Cultura from df"): Verificar os níveis do fator Cultura

Para o fator Estádio nós temos: V5, V7 e V8.

Enquanto para Cultura nós temos: Milhoconv; MilhoBt e Urochloa

Vamos comparar primeiro os estádios dentro de cada cultura.

Primeiro, faremos um subset dentro de cada cultura:

EstadiosMC<-subset(df, df$Cultura=="Milhoconv")

EstadiosMBt<-subset(df, df$Cultura=="MilhoBt")

EstadiosU<-subset(df, df$Cultura=="Urochloa")

Depois, precisaremos criar um modelo para cultura

Modelo.EstadiosMC<-glm(SfrugTot~Estadio+Bloco, family= "poisson", data=EstadiosMC)

Modelo.EstadiosMBt<-glm(SfrugTot~Estadio+Bloco, family= "poisson", data=EstadiosMBt)

Modelo.EstadiosU<-glm(SfrugTot~Estadio+Bloco, family= "poisson", data=EstadiosU)

Para realizar as comparações, nós precisaremos do pacote "multcomp" [7], para isso vamos rodar a linha de comando (ela irá carregar ou instalar o pacote, caso necessário):

if(!require(multcomp)){install.packages("multcomp")}

Modelo para os dados de milho convencional:

Comp.EstadiosMC<-summary(glht(Modelo.EstadiosMC,linfct=mcp(Estadio="Tukey")))

Modelo para os dados de milho Bt:

Comp.EstadiosMBt<-summary(glht(Modelo.EstadiosMBt, infct=mcp(Estadio="Tukey")))

Modelo para os dados de Urochloa:

Comp.EstadiosU<-summary(glht(Modelo.EstadiosU, linfct=mcp(Estadio="Tukey")))

Resultados das comparações na forma de probabilidade:

(Comp.EstadiosMC<-summary(Comp.EstadiosMC, test = univariate()))

(Comp.EstadiosMBt<-summary(Comp.EstadiosMBt, test = univariate()))

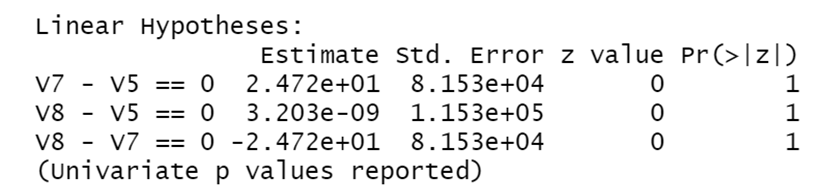
(Comp.EstadiosU<-summary(Comp.EstadiosU, test = univariate()))

A partir dos resultados das comparações na forma de probabilidade podemos notar que houve diferença significativa apenas na terceira comparação em "V8 - V5" e "V8 - V7".

Para visualizar de forma mais clara, é possível atribuir letras para as diferenças significativas, com os comando a baixo:

(Letras.EstadiosMC<-cld(Comp.EstadiosMC, level=0.05, Letters= c(LETTERS, letters), decreasing=TRUE))

(Letras.EstadiosMBt<-cld(Comp.EstadiosMBt, level=0.05, Letters= c(LETTERS, letters), decreasing=TRUE))

(Letras.EstadiosU<-cld(Comp.EstadiosU, level=0.05, Letters= c(LETTERS, letters), decreasing=TRUE))

Com a atribuição de letras podemos confirmar a diferença estatística que ocorre na última comparação.

Agora vamos comparar as culturas dentro de cada estádio.

Faremos um subset dentro de cada estádio:

CulturasV5<-subset(df, df$Estadio=="V5")

CulturasV7<-subset(df, df$Estadio=="V7")

CulturasV8<-subset(df, df$Estadio=="V8")

Posteriormente, necessitaremos criar um modelo para cada estádio.

Modelo.V5<-glm(SfrugTot~Cultura+Bloco, family= "poisson", data=CulturasV5)

Modelo.V7<-glm(SfrugTot~Cultura+Bloco, family= "poisson", data=CulturasV7)

Modelo.V8<-glm(SfrugTot~Cultura+Bloco, family= "poisson", data=CulturasV8)

Vamos realizar as comparações utilizando o mesmo método anterior, só contrastando o fator "Cultura".

Comp.CulturasV5<-summary(glht(Modelo.V5, linfct=mcp(Cultura="Tukey")))

Comp.CulturasV7<-summary(glht(Modelo.V7, linfct=mcp(Cultura="Tukey")))

Comp.CulturasV8<-summary(glht(Modelo.V8, linfct=mcp(Cultura="Tukey")))

Resultados das comparações na forma de probabilidade:

(Comp.CulturasV5<-summary(Comp.CulturasV5, test = univariate()))

(Comp.CulturasV7<-summary(Comp.CulturasV7, test = univariate()))

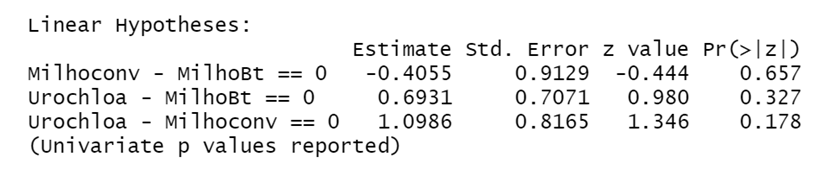
(Comp.CulturasV8<-summary(Comp.CulturasV8, test = univariate()))

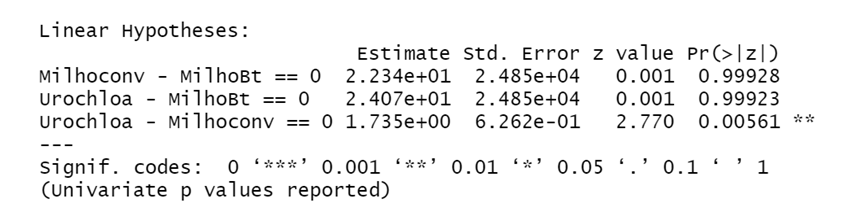
A partir dos resultados das comparações na forma de probabilidade podemos notar que houve diferença significativa apenas na primeira comparação em "Urochloa - Milhoconv" e na ultima comparação em "Urochloa - Milhoconv".

Para visualizar de forma mais clara, é possível atribuir letras para as diferenças significativas, com os comando a baixo:

(Letras.CulturasV5<-cld(Comp.CulturasV5, level=0.05, Letters= c(letters, letters), decreasing=TRUE))

(Letras.CulturasV7<-cld(Comp.CulturasV5, level=0.05, Letters= c(letters, letters), decreasing=TRUE))

(Letras.CulturasV8<-cld(Comp.CulturasV5, level=0.05, Letters= c(letters, letters), decreasing=TRUE))

Com a atribuição de letras podemos confirmar a diferença estatistica que ocorre na ultima comparação.

Agora vamos realizar uma análise descritiva, para isso precisamos do pacote "Rmisc" [2]. Vamos rodar a linha de comando a baixo, ela instalará o pacote, caso necessário.

if(!require(Rmisc)){install.packages("Rmisc")}: vamos utilizar o pacote "Rmisc"

Em seguida, fazemos um "summary", para visualizar um resumo da análise:

summarySE(df, measurevar = "SfrugTot", groupvars = c("Estadio", "Cultura"))

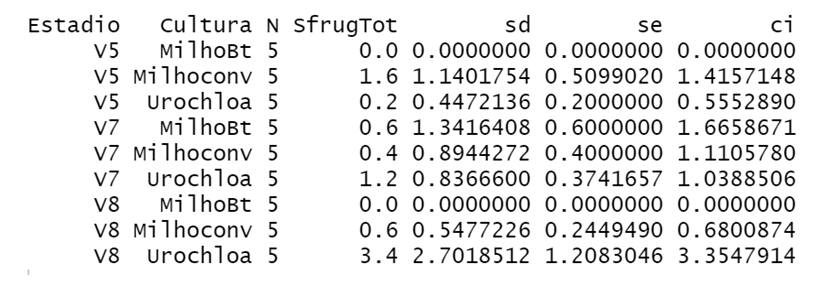
Os valores que não possuem variabilidade não podem ser considerados nas compara-ções. Os valores obtidos a partir da análise descritiva pode ser colocada em uma tabela da seguinte forma:

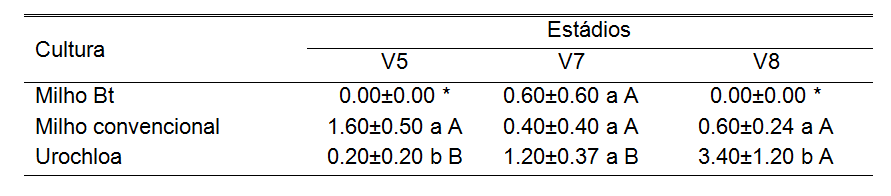
Letras minúsculas comparam culturas dentro do fator estádio (comparação dentro das colunas), enquanto letras maiúsculas comparam estádios dentro de cada cultura (comparação dentro das linhas). *Como não houve variabilidade nesse tratamento, o mesmo não será considerado nas comparações.

Anexo - Banco de Dados 1

Host

Rep

y

Brachiaria

1

13

Brachiaria

2

20

Brachiaria

3

24

Brachiaria

4

17

Brachiaria

5

22

Brachiaria

6

2

Brachiaria

7

17

Brachiaria

8

15

Brachiaria

9

26

Brachiaria

10

19

Crotalaria

1

36

Crotalaria

2

50

Crotalaria

3

1

Crotalaria

4

34

Crotalaria

5

2

Crotalaria

6

48

Crotalaria

7

6

Crotalaria

8

45

Crotalaria

9

27

Crotalaria

10

6

Algodão

1

216

Algodão

2

180

Algodão

3

197

Algodão

4

124

Algodão

5

180

Algodão

6

281

Algodão

7

203

Algodão

8

100

Algodão

9

228

Algodão

10

239

Soja

1

29

Soja

2

4

Soja

3

61

Soja

4

50

Soja

5

34

Soja

6

77

Soja

7

84

Soja

8

70

Soja

9

103

Soja

10

71

Milho

1

222

Milho

2

218

Milho

3

373

Milho

4

400

Milho

5

478

Milho

6

454

Milho

7

400

Milho

8

263

Milho

9

472

Milho

10

382

Guandu

1

2

Guandu

2

2

Guandu

3

4

Guandu

4

0

Guandu

5

2

Guandu

6

0

Guandu

7

5

Guandu

8

3

Guandu

9

0

Guandu

10

1

Mucuna Preta

1

0

Mucuna Preta

2

0

Mucuna Preta

3

0

Mucuna Preta

4

2

Mucuna Preta

5

4

Mucuna Preta

6

0

Mucuna Preta

7

1

Mucuna Preta

8

1

Mucuna Preta

9

5

Mucuna Preta

10

3

Sorgo

1

2

Sorgo

2

0

Sorgo

3

5

Sorgo

4

4

Sorgo

5

0

Sorgo

6

4

Sorgo

7

0

Sorgo

8

0

Sorgo

9

1

Sorgo

10

0

Girassol

1

2

Girassol

2

0

Girassol

3

1

Girassol

4

0

Girassol

5

1

Girassol

6

0

Girassol

7

0

Girassol

8

0

Girassol

9

1

Girassol

10

1

Pousio

1

0

Pousio

2

0

Pousio

3

1

Pousio

4

0

Pousio

5

1

Pousio

6

0

Pousio

7

0

Pousio

8

0

Pousio

9

0

Pousio

10

0

6. Referências dos pacotes utilizados

[1] Wickham H., Bryan J. readxl: Read Excel Files. R package version 1.3.1. 2019. https://CRAN.R-project.org/package=readxl

[2] Hope, R.M. Rmisc: Rmisc: Ryan Miscellaneous. R package version 1.5. https://CRAN.R-project.org/package=Rmisc. 2013.

[3] Venables W.N., Ripley B. D. Modern Applied Statistics with S. Fourth Edition. Springer, New York. 2002.

[4] Moral, R.A., Hinde, J., Demétrio, C.G.B. Half-normal plots and overdispersed models in R: The hnp package. Journal of Statistical Software, v. 81, n. 10, 2017.

[5] Demétrio, C.G.B. Modelos lineares generalizados em experimentação agronômica. USP/ESALQ, 2001.

[6] Demétrio, C.G., Hinde, J., Moral, R.A. Models for overdispersed data in entomology. In: Ecological modelling applied to entomology. Springer, Cham, 2014. p. 219-259.

[7] Hothorn, T., Bretz F., Westfall P. Simultaneous inference in general parametric models. Biometrical Journal 50(3), 346--363. 2008.

[8] Grothendieck, G. sqldf: Manipulate R Data Frames Using SQL. R package version 0.4-11. https://CRAN.R-project.org/package=sqldf. 2017.


7. Referências dos pacotes utilizados

Demétrio, C.G.B. Modelos lineares generalizados em experimentação agronômica. USP/ESALQ, 2001.

Demétrio, C.G., Hinde, J., Moral, R.A. Models for overdispersed data in entomology. In: Ecological modelling applied to entomology. Springer, Cham, 2014. p. 219-259.


Autores

José Bruno Malaquias, Instituto de Biociências - Campus de Botucatu. R. Prof. Dr. Antônio Celso Wagner Zanin, 250 - Distrito de Rubião Junior - Botucatu/SP, Brasil - CEP 18618-689

Jéssica Karina da Silva Pachú, Departamento de Entomologia e Acarologia - LEA Avenida Pádua Dias, 11 - CEP 13418-900 - Piracicaba/SP, Brasil

Filipe Lemos Jacques, Universidade Federal da Grande Dourados - Unidade I: Rua João Rosa Góes, nº 1761, Vila Progresso, Dourados/ MS, Brasil, CEP: 79825-070

Paulo Eduardo Degrande, Universidade Federal da Grande Dourados - Unidade I: Rua João Rosa Góes, nº 1761, Vila Progresso, Dourados/ MS, Brasil, CEP: 79825-070

* Autor para correspondência: malaquias.josebruno@gmail.com